コマ大数学科9月24日放送(日付はサンテレビ)の問題です。1966年京都大学入試問題かららしいです。(問題文は一字一句忠実ではありません。)

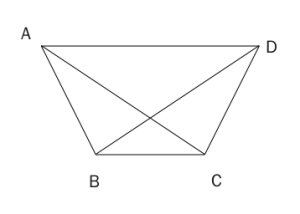
平面上に相異なる4点がある。そのうち、どの3点をとっても正三角形にはならない。2点間の距離が、1,1,1,a,a,a のとき、a の値を求めよ。ただしa >1とする

図のように4点がなる場合が答えで、AB=BC=CD=1, AC=BD=AD=aとなります。(入試問題なら、これ以外に無い、ということも証明する必要がありそうですが、コマ大ではそこまで要求されていなかったようです。)

後は a をどうやって求めるかですが、台形ということで、角ABCと角BADの和=180 (*)を利用します。
余弦定理から、
1+1-2a cos(ABC) = a²
1+a²-2a cos(BAD) = a²
(*) から、cos(ABC) = -cos(BAD) を用いて整理すると、
(a-1)(a²+a-1)=0
a > 1 を満たす答えは、a = ½(1+√5) となります。

マス北野は正五角形、黄金比に気付き、京大生東田大志さんより早く解きました。炎天下で話しながら9分52秒というタイムもすごいですが。東大生チーム（衛藤樹さん、伊藤理恵）は、cos36 までたどり着いたのですが、時間切れとなってしまいました。